PMVS论文随笔（1）

发表于 更新于 分类于

关于Unit的概念

在pmvs的源代码中，有一个函数是getUnit ，其函数如下（在PMVS2的windows版本代码，optim.cc文件，1184行）：

1
2
3
4
5
6
7
8
float Coptim::getUnit(const int index, const Vec4f& coord) const {
  const float fz = norm(coord - m_fm.m_pss.m_photos[index].m_center);
  const float ftmp = m_ipscales[index];
  if (ftmp == 0.0)
    return 1.0;

  return 2.0 * fz * (0x0001 << m_fm.m_level) / ftmp;
}

其中index是图像编号，coord是三维射影空间下的坐标。

这个函数在pmvs代码中几乎所有的和空间几何计算相关的函数中均被调用，最开始看代码时我并没有特别注意，但是随着代码阅读的深入，发现如果不将该函数读懂，就完全无法理解pmvs中所有的几何计算函数究竟是在做什么，于是今天花时间特意钻研了下，把该函数的含义表达清楚。

先说结论：该函数是计算将图片上的一个像素反投影到空间的一个指定的面片（patch）上得到的正方形的大小（以世界坐标系中的距离为量度），这个面片满足如下条件——面片的中心位于coord， 面片的法线与相片的法线平行但方向相反（也就是论文中初始化patch时的法线计算方法）。

这个结论看起来非常复杂，简单说就是如果我在空间的某个坐标处想要画一个正方形，使得该正方形投影到对应的与该正方形平行的相片上的大小恰好是1×1像素大小，那么这个正方形的边长在世界坐标系中的表达究竟是多少。这个函数就是来求解这个边长的。

这样的话这个函数作用其实就相当大了，他直接沟通了像素坐标和空间坐标的比例关系，可以粗略的比较相片对于场景的缩放，简化很多投影和反投影计算。而这个函数用到的计算方法其实也非常简单。就是简单的相似三角形关系，具体解释如下

小孔成像相机的几何关系如下图所示（摘自《 Multiple View Geometry in Computer Vision 》）

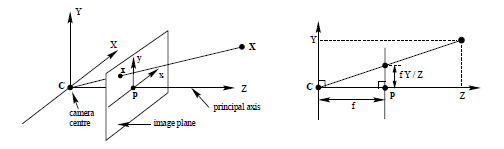
从该成像原理上我们可以看出，空间中一个长度为\(D\) 的物体投影到图像上长度\(l\)满足如下关系： \[ \frac{D}{l} = \frac{Z_0}{f} \] 其中\(f\) 为焦距，\(Z_0\) 为物体到摄影中心的距离。 由上式可以得到： \[ D = \frac{l}{f}Z_0 \] 这样我们已知\(l\) 为1个像素长度，\(Z_0\) 可以直接由coord到相片的摄影中心直接计算得到。那么只要我们知道以像素为单位的\(f\)的数值，就可以直接得到\(D\)。幸运的是，根据一般CCD相机内参数矩阵中各变量的定义： \[ K=\begin{bmatrix} a_x & s & x_0 \\ 0 & a_y & y_0 \\ 0 & 0 & 1 \end{bmatrix} \] 其中\(a_x\)和 \(a_y\)分别是相机在x和y方向上的焦距，且以像素为量纲。另外一般情况下，CCD相机在x和y方向上的比例因此近似相等，即\(a_x \approx a_y\)，这样我们可以用下式来近似计算\(f\) \[ f = \frac{a_x + a_y}{2} \] 综上可得： \[ D=\frac{2}{a_x + a_y} Z_0 \] 这就是pmvs中getUnit的计算方法， 特别解释下，代码中m_ipscales[index]就是提前计算好的\(a_x+a_y\)的数值，而(0x0001 << m_fm.m_level)则是一个比例因子，可以让程序将图像缩放到一半或者四分之一大小进行计算。